
One of the common problems that involve an isosceles triangle includes an altitude drawn to the base. Some definitions allow for you to prove that two angles are congruent, some need the extra step to show that two sides are congruent. Make sure to note the definition given to you for what an isosceles triangle is. These two theorems are important for any proofs that ask you to prove a triangle is an isosceles triangle. Once more the congruent angles form the base and the congruent sides are the legs. If we know that two angles are congruent, or have the same measure, than we know that the opposite sides are congruent, or have the same length. Theorem #2 (converse) – If two angles of a triangle are congruent, the sides opposite them are congruent. The converse of this theorem looks at the reverse. Notice that the base of the triangle is created by both angles that are congruent. The arcs that are in the angles are indicating that the angles have the same measure, or are congruent. The single lines on the legs of the isosceles triangles are tick marks indicating that the sides have the same length, or are congruent. To find the opposite angle you want to look at the angle that the side is not a part of.
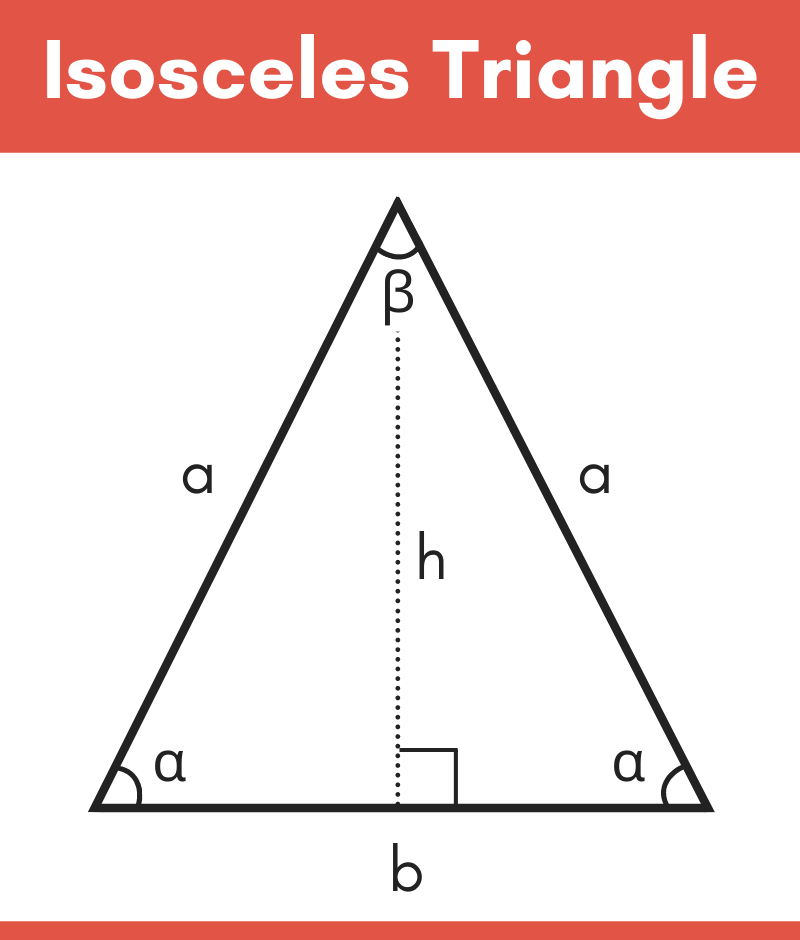
This means that if we know that two sides are congruent in a triangle, we know that two angles are congruent as well. Isosceles Triangle Theorems Theorem #1 – If two sides of a triangle are congruent, the angles opposite them are congruent.
Vertex angle of an isosceles triangle how to#
Now let’s see how to find the missing sides of an isosceles triangle and calculate their lengths. Knowing that an isosceles triangle has two sides that are equal leads us to the first theorem that is associated with isosceles triangles. Oftentimes a problem will use this vocabulary to give information. The two sides that are the same length are referred to as the legs and the third side is called the base. Often abstract or complicated shapes are broken into smaller shapes such as a triangle. Many triangles found in the real world can be considered isosceles, including a section of a slice of pizza. Isosceles Triangle Properties, Characteristics & Uses These words make a difference when considering if a triangle is also an equilateral triangle as well as an isosceles triangle.

Theorem #1 – If two sides of a triangle are congruent, the angles opposite them are congruent.Isosceles Triangle Properties, Characteristics & Uses.


 0 kommentar(er)
0 kommentar(er)
